Kinetic Monte Carlo

Monte Carlo methods are a way of numerically simulating physical processes by repeatedly sampling random numbers. The classic example is estimating the value of pi. You randomly generated a large number of (x,y) points between 0 and 1, and count how many fall within a circle centered at (0, 0). The ratio of interior points to total points is the same as the ratio of the area of a circle quadrant to the area of the full 1 x 1 square, which is pi/4.

But we can also simulate systems that evolve over time. For a given state, we know the probabilities of transitioning to a new state. So at each time step, we generate a random number and use this and the probabilities to choose which transition should occur. Imagine we want to simulate the growth of a thin film of material deposited from the vapor phase. We can consider two processes: new atoms from the vapor phase adsorb onto a lattice site on the surface, and already adsorbed atoms may diffuse along the surface.

Our state is the postitions of all atoms on the surface. Possible transitions are an atom hopping from one site to another. We spawn more particles on the surface to simulate a flux of vapor depositing more atoms. The hopping probabilities depend on whether the atom has a nieghbor, or if it will be moving 'down' a layer (the energy cost of this can be higher than moving 'along' a layer and is known as the Ehrlich–Schwoebel barrier.)

So we can write a simple simulation loop where we:

List the possible transitions with their rates
Generate a random number
Use the random number to choose a transition
Carry out the transition (i.e., move an atom to a new location)
Update the time based on the rate of the selected transition

We also make some simplifying assumptions. I'm just going to do this in two dimensions and a square lattice. A real system would obviously be three dimensional, and simple cubic lattices are rare in nature.

To start, let's define our possible transition types and assign them some probabilties:

from enum import Enum

class TransitionType(Enum):
    DIFFUSE = 1
    HOP_DOWN = 2
    DEPOSIT_NEW = 3
transition_rates = {
    TransitionType.DIFFUSE: 0.2,
    TransitionType.HOP_DOWN: 0.25,
    TransitionType.DEPOSIT_NEW: 0.35,
}

For our toy model, these are arbitrary. But their relative values tell us something about the system. Turning up the probability of a deposition event is like increasing the deposition rate (in our hypothetical thin film deposition process), while the surface diffusion rate depends on the temperature.

Now we can write our simulation loop. Each step, we need to list all the possible transitions. Depositing a new particle is always a possibility. And then, each particle that does not have an immediate neighbor can diffuse left or right, potentially hopping down to a lower level. We add up the probabilities of each transition and then generate a random number to choose which transition will happen.

First, we add the transition for a new particle being deposited. Just pick a random x-coordinate and find the lowest unoccupied site:

x = random.randint(0, WIDTH)
 y = 0
 while (x, y) in self.particles:
     y += 1
possible_transitions = [{'src': None, 'dst': (x, y), 'type': TransitionType.DEPOSIT_NEW}]

I'm storing transition events as simple dicts with a source, destination so we know which particle sites to update. Now we add the rest of the possible transitions for the existing particles. We assume that if a neighboring site is occupied, the particles bond to each other and won't move. Likewise, a particle in a lower layer that has a higher layer growing on top cannot move. Otherwise, if there is an open neighboring site that is supported by a particle layer (or bare substrate) below, a particle can diffuse laterally, or hop down one layer.

for x,y in self.particles:
    left = x - 1 % WIDTH
    right = x + 1 % WIDTH
    up = y + 1
    down = y - 1
    if (left, y) in self.particles or (right, y) in self.particles or (x, up) in self.particles:
        # Bonded to a neighbor, won't move
        continue
    if (left, down) in self.particles or down < 0:
        possible_transitions.append({'src': (x,y), 'dst': (left, y), 'type': TransitionType.DIFFUSE})
    if (right, down) in self.particles or down < 0:
        possible_transitions.append({'src': (x,y), 'dst': (right, y), 'type': TransitionType.DIFFUSE})
    if (down == 0 or (left, down - 1) in self.particles) and not (left, down) in self.particles:
        possible_transitions.append({'src': (x,y), 'dst': (left, down), 'type': TransitionType.HOP_DOWN})
    if (down == 0 or (right, down - 1) in self.particles) and not (right, down) in self.particles:
        possible_transitions.append({'src': (x,y), 'dst': (right, down), 'type': TransitionType.HOP_DOWN})

Now we generate a random number to choose one of these transitions. I'm just doing a linear scan, but it would be best to use binary search to more quickly find the right transition:

total_prob = sum([transition_rates[t['type']] for t in possible_transitions])
choice = total_prob * random.random()
i, cum_prob = 0
while i < len(possible_transitions):
    cum_prob += transition_rates[possible_transitions[i]['type']]
    if choice < cum_prob:
        transition = possible_transitions[i]
        break
    i +=1

With our next transition chosen, we simply update the particle list.

self.particles.append(transition['dst'])
if transition['type'] != TransitionType.DEPOSIT_NEW:
    self.particles.remove(transition['src'])

And that's it. We have a minimal, working simulation. Add some visualization, and play with the parameters. Turn up the deposition rate so it is must faster than diffusion, and we get a rougher film surface:

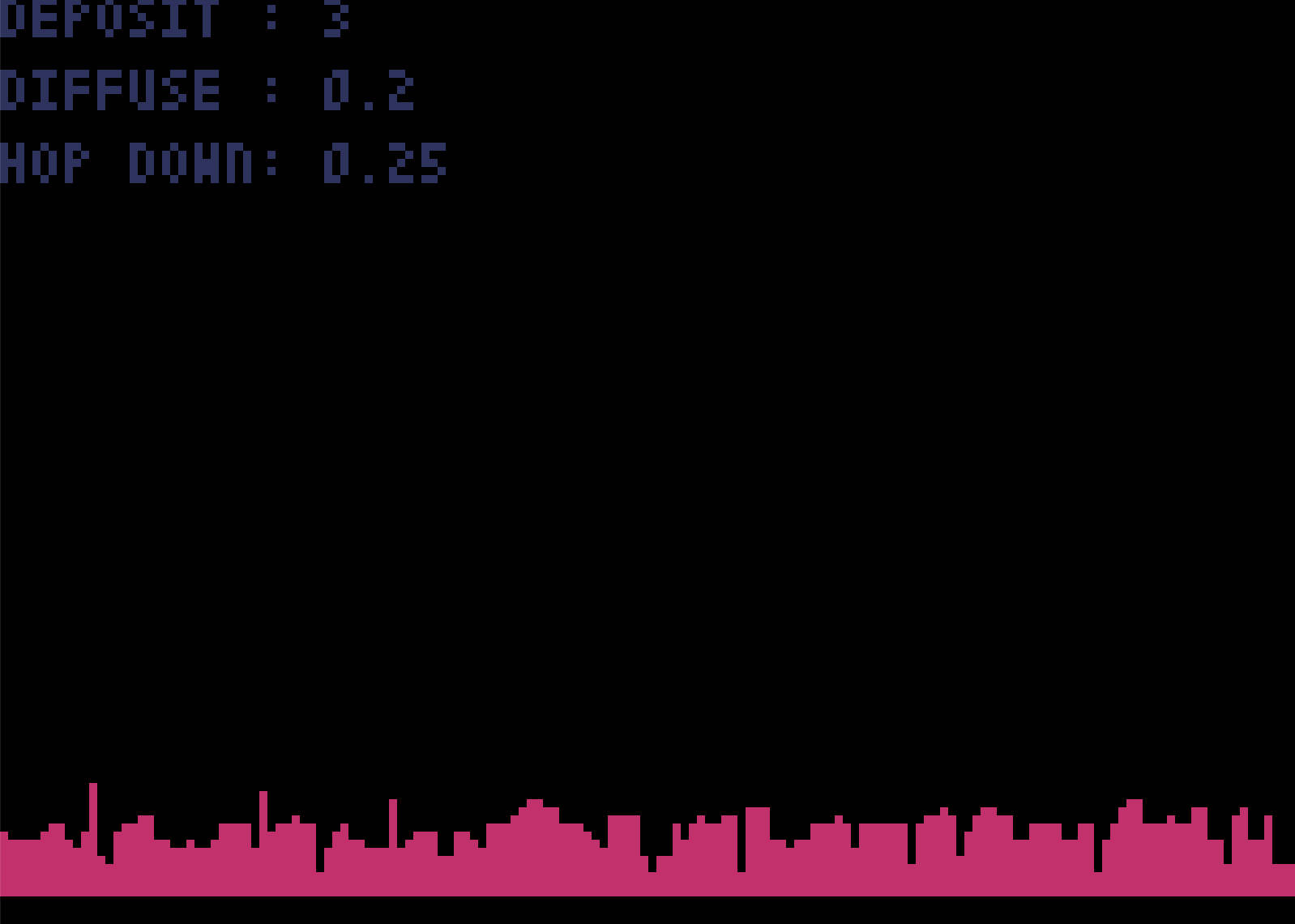
Turn the deposition rate down, so the particles have more time to diffuse and find each other, and we get a smoother film:

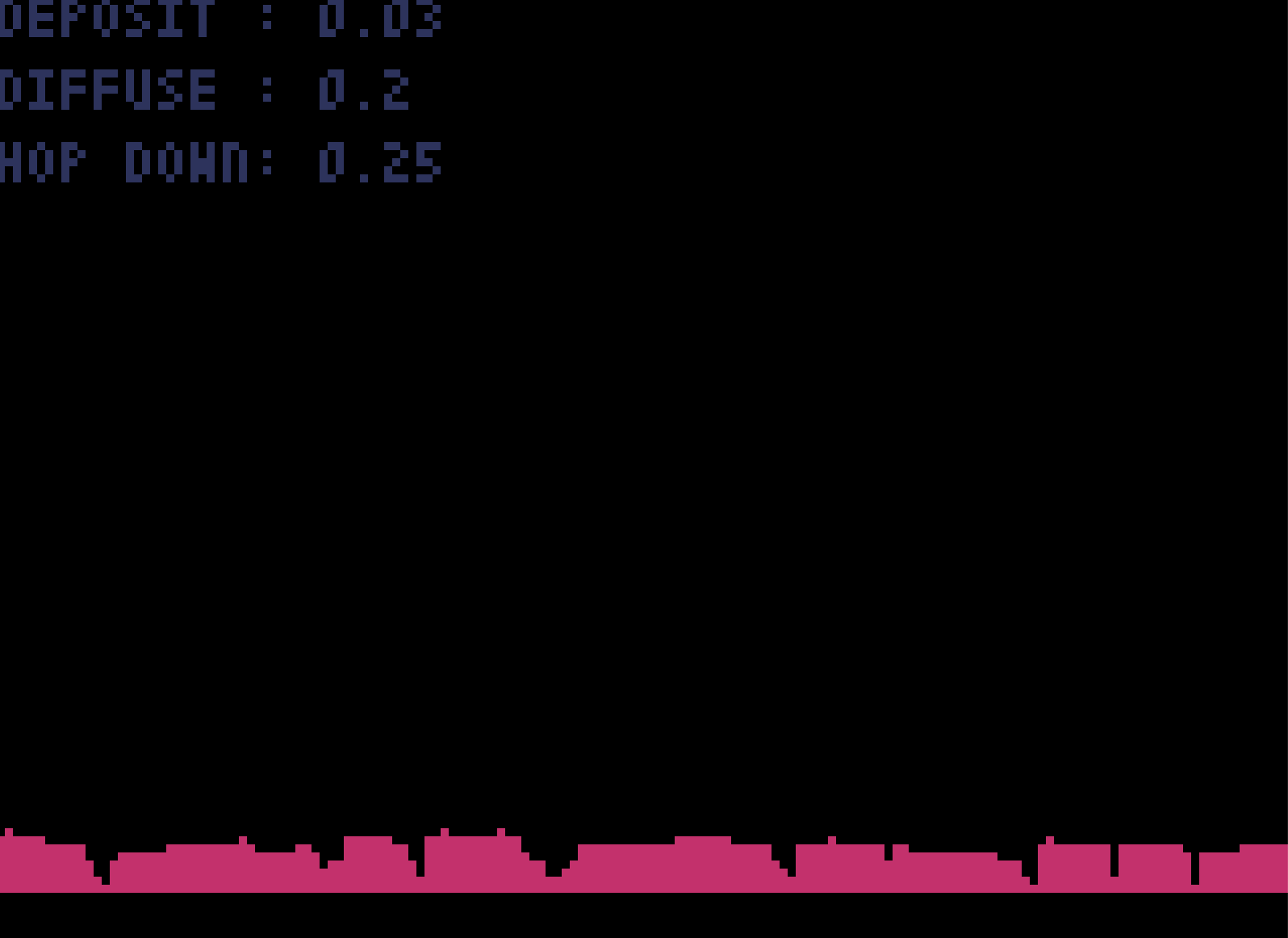
Full code for my toy sim and visualization using pyxel is on github. I adjust the speed of the animation by just doing multiple simulation steps in the pyxel update() function. Let it go on for a while and it slows down noticably. There's a few places this could be optimized for better performance. Adding and removing particles from a python list is going to be O(n). It would be better to simply use something like a numpy 2D array and just keep track of whether that grid space is occupied. Setting an array element to 1 or 0 is a nice O(1) operation. We're also doing linear scan instead of binary search for choosing a transition, so that's another O(n) operation we can improve. It's also probably not necessary to recalculate the entire transition list every step, since only one particle is being moved each step, only the transitions related to that one particle need to be updated.